
X = np.broadcast_to( np.arange( y.shape ), y.T.shape ).T # axis with values to reduce must be trailing for broadcast_to, # note that the axis 'vanishes' anyways, so we don't need to swap it back # as is necessary for subtraction of the means # move axis we wanna calc the slopes of to first # spaced y-values (like in numpy plot command) # assume that the given single data argument are equally import numpy as npĭef calcSlopes( x = None, y = None, axis = -1 ): So, if you have arbitrary tensors X, Y and you want to know the slopes for all other axes along the data in the third axis, you can call it with calcSlopes( X, Y, axis = 2 ). It will calculate the slopes of the data along the given axis. I built upon the other answers and the original regression formula to build a function which works for any tensor. Slope_2, intercept, r_value, p_value, std_err = stats.linregress(X, Y) Slope_1, intercept, r_value, p_value, std_err = stats.linregress(X, Y) Slope_0, intercept, r_value, p_value, std_err = stats.linregress(X, Y) I also don't think linregress is the best way to go because I don't need any of the auxiliary variables like intercept, standard error, etc in my results.

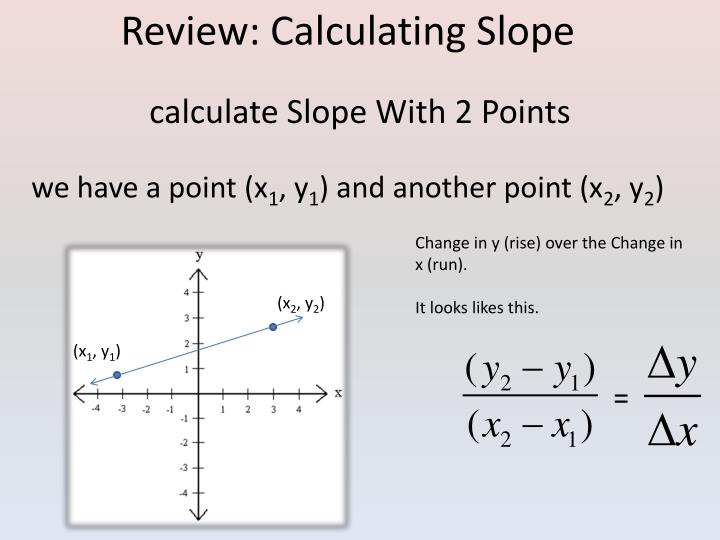
For example, I can easily do this one row at a time, as shown below, but I was hoping there was a more efficient way of doing this. I have a data set of three Y variables and one X variable and I need to calculate their individual slopes. I am trying to find the fastest and most efficient way to calculate slopes using Numpy and Scipy.


 0 kommentar(er)
0 kommentar(er)
